[ML/DL] 소프트맥스 회귀(Softmax regression)

 

저번 포스팅에서는

합격/불합격과 같은 이진 분류 문제를 푸는 로지스틱 회귀에 대해 알아보았다.

 

오늘은

이진 분류를 넘어서

3개 이상의 선택지 중에서 하나를 고르는

다중 클래스 분류 문제를 위한

소프트맥스 회귀(Softmax regression)에 대해 알아보자!

 

---

 

다중 클래스 분류(Multi-class Classification)

 

로지스틱 회귀에서는

시그모이드 함수를 사용하여 입력값에 대한 출력을

0과 1사이의 값으로 출력해준다.

 

따라서

"0.5가 넘으면 합격, 넘지 못하면 불합격"

과 같이 판단 또한 해줄 수 있었다.

 

하지만 합/불이 아닌

A,B,C 학점으로 나누어 준다고 할 때

시그모이드 함수를 사용한다면,

A 학점을 받을 확률, B 학점을 받을 확률, C 학점을 받을 확률을

각각 출력해줄 것이며 그 확률의 합이 1이 아닐 수가 있다.

 

이럴때 사용할 수 있는 것이

바로 소프트맥스 함수!

 

---

 

소프트맥스 함수(Softmax function)

https://wikidocs.net/35476

 

일단 수식은 위와 같다!

 

시그모이드 함수와 비교했을 때,

소프트맥스 함수의 장점은

1. 시그모이드 함수에 비해 Saturation 문제가 비교적 줄어든다.
2. 상대적인 평가가 가능하다.(합을 1로 표현)
3. 자연로그 e를 사용함으로써 더욱 두드러진 값들로 표현 가능하다.

3가지로 설명하는데...

 

saturation 하다라는 표현이 이해가 안간다.

검색을 해보니 원래 신호에 성분이 더해져 소리가 왜곡되는 현상이라고 나오는데,,

AI에서는

 

작은 기울기는 곧 학습 능력이 제한된다는 것을 의미하고 이를 일컬어 신경망에 포화(Saturation)가 발생했다고 한다.

라는 의미에서 쓰인다고 한다!

 

 

그렇다면,

어떤 방식으로 계산이 될까?

 

https://wikidocs.net/35476

 

원-핫 벡터는

클래스를 분류할 때,

정수 인코딩처럼 0,1,2가 아닌 [1,0,0] , [0,1,0], [0,0,1]과 같이 표현하는 것이다.

 

이렇게 표현하는 이유는

다중 클래스 분류 문제가 클래스 간의 관계가 균등하기 때문에

정수 인코딩 보다는 원-핫 벡터가 적절하다.

 

또한 예시에서 입력 벡터는 4차원인데,

계산된 z벡터는 3차원으로 표현되고 있다.

https://wikidocs.net/35476

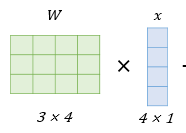
이는 입력 벡터와 가중치 w를 곱할 때,

출력 값의 차원을 축소하여 z를 3차원으로 표현하는 것이다.

 

그리고 실제 값과 예측 값의 오차로부터

가중치 w와 편향 b를 업데이트 해준다.

 

https://wikidocs.net/35476

따라서

소프트맥스 회귀에서 예측 값을 구하는 과정은

위의 그림과 같을 것이다!

 

---

 

크로스 엔트로피(Cross Entropy Function)

 

정보 이론에서

엔트로피(Entropy)는

정보를 표현하는데 필요한 최소 평균 자원량

이라고 한다.

 

정보 이론의 아버지,

클로드 섀넌은 정보를 표현하는 단위를 bits라고 정의하고

곧, 짧게 표현하는 것의 평균이 엔트로피가 되겠다.

 

영상 속 예시가 매우 직관적이여서

이해하기가 쉬웠다.

 

https://www.youtube.com/watch?v=z1k8HVU4Mxc&list=PL_iJu012NOxdDZEygsVG4jS8srnSdIgdn&index=12

 

[좌측 사진]

연인과의 채팅 속에서

ㅗ 보다는 하트 이모티콘이 더욱 자주 쓰일 것이다.

하지만 ㅗ 도 오타로 칠 수도 있을거지만 비교적 확률이 적을 것이다!

 

[우측 사진]

따라서 나올 확률이 적은 값에겐

상대적으로 긴 bit의 표현을 할당하고

나올 확률이 높은 하트에게는

짧은 bit의 표현을 할당해야,,

 

자원을 효율적으로 사용하는게 될거다!

 

때문에 우측 사진과 같은 그래프가 필요할 것이고

우측 그래프의 수식

이다. p는 확률!

 

이게바로 엔트로피 함수(Entropy Function) 이다.

 

 

 

여기에 실제값 y와 클래스의 개수 k, 내가 생각한 확률 분포인 p를 정의한 표현식이

https://wikidocs.net/35476

크로스 엔트로피 함수(Cross Entropy Function)이며,

엔트로피 함수 보다는 비교적 비효율적인 함수가 될 것이다!

 

왜냐!

엔트로피 함수가 가장 미니멈이기 때문,,

 

 

 

여기서 크로스 엔트로피(CEN) - 엔트로피(EN)를 해주면

얼마나 비효율적인가를 알 수 있고

그것이 바로 KL-divergence라고 한다.

 

https://www.youtube.com/watch?v=z1k8HVU4Mxc&list=PL_iJu012NOxdDZEygsVG4jS8srnSdIgdn&index=12

추가적으로

x와 y가 실제로는 독립이 아닌데,

독립이라고 생각하고 코딩을 했을 때의 비효율성을

Mutual information이라고 한다..

 

때문에 독립이 아닌 정도가 클수록

값 또한 커진다.

 

 

이야기가 좀 옆으로 빠졌지만,

 

 

 

결론은!!

로지스틱 회귀의 비용 함수도 크로스 엔트로피,

소프트맥스 회귀도 크로스 엔트로피 였다.

때문에 소프트맥스 회귀의 최종 비용 함수에서 k가 2라고 가정하면,

로지스틱 회귀의 비용 함수와 같다.

 

 

끝.

 

참고자료

혁펜하임 - 딥러닝 3.3강

혁펜하임 - 딥러닝 4강

딥러닝을 이용한 자연어 처리 입문