| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- lock based stack
- render target
- 홀짝트리
- c++
- 2025 프로그래머스 코딩챌린지 1차예선
- boj 21921
- LCS
- dp
- lock based queue
- boj 11053
- PCCE
- 데이터 체커
- orthographic projection
- 비밀 코드 해독
- boj 15724
- DirectX12
- 색종이와가위
- boj 6443
- boj 22942
- boj 1074
- boj 1958
- pccp 기출문제 풀이
- tessellation
- boj 20207
- 브루트포스
- 프로그래밍공부
- DirectX
- pcce 기출문제 풀이
- 지게차와 크레인
- lock free stack
- Today
- Total
오구의코딩모험
[ML/DL] 선형 회귀(Linear Regression)란? 본문

딥러닝 공부에 앞서
머신러닝부터 공부해보자
오늘은 머신러닝의 기초인
선형 회귀에 대해 알아보겠다.

선형 회귀(Linear Regression)
선형 회귀는 한 개 이상의 독립 변수 x와 y의 선형 관계를 모델링 하는 것
이라고 하는데, 이게 무슨 뜻일까?
예를 들어보자


좌측의 사진은
어떤 학생의 공부 시간에 따른 점수를 나타낸 데이터다.
현재는 5시간 했을 때가 최대인데,
그럼 6시간을 공부했다면 점수는 몇 점일지 궁금하다.
정확하진 않겠지만 우측 사진과 같이
선을 그어 5시간을 초과했을 때의 점수도 예측해볼 수 있을 것이다.
이렇게 선을 그어 예측을 해보기 위해
수학적으로 수식을 세우게 되는데

머신러닝에서는 이러한 식을 가설(Hypothesis)이라 한다.
즉,
선형회귀는 주어진 데이터로 부터
y와 x의 관계를 가장 잘 나타내는 직선을 그리는 일이라고 볼 수 있다!
꼭 직선이 아니여도 된다!

선형 회귀에서 선형은
파라미터에 대해서 선형이냐,
가 중요한 것이지
그려진 그래프가 직선이기 때문에 선형인건 아니다!
그렇다면
y와 x의 관계를 잘 나타내는 방법은 뭘까?
오차의 최소화
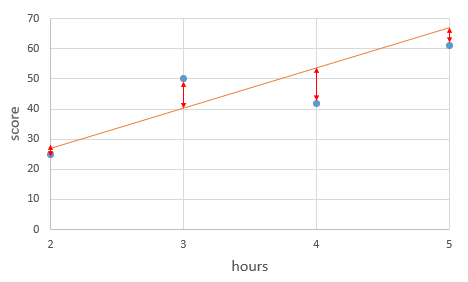
실제값과 가설로부터 얻은 예측값의 오차를 최소로 해야한다!
실제값과 예측값 오차에 대한 식을
비용 함수(Cost Function) 또는 손실 함수(Loss Function)라고 말한다.
손실 함수에는 여러가지 함수가 있지만,
오늘 다루고 있는 회귀 문제의 경우
주로 평균 제곱 오차(Mean Squared Error, MSE)가 사용된다.
평균 제곱 오차?
단어 그대로 해석하면,
오차를 제곱해서 평균을 내는 것 같은데,,
왜 제곱을 해주고 평균을 낼까?
위의 사진을 보면,
직선 위의 오차와 직선 아래의 오차는
(+),(-) 부호가 반대기 때문에
그냥 더해주면 오차의 합이 작아지거나, 0이 될 수 있다.
이런 경우를 방지하기 위해
+,- 부호를 지우고자 제곱을 해주는 것!
옵티마이저(Optimizer)

결국
평균 제곱 오차가 최소가 되는 w와 b를 구한다면,
y와 x의 관계를 가장 잘 나타내는 직선을 그릴 수 있다.
그러기 위해서는 적절한 w와 b를 찾아야 한다.
최적의 w와 b는 어떻게 찾을 수 있을까?
이때 사용되는 알고리즘을 옵티마이저(Optimizer) 또는 최적화 알고리즘이라고 부른다.
옵티마이저를 통해 적절한 w와 b를 찾아내는 과정을 머신 러닝에서 훈련(training) 또는 학습(learning)이라 한다.
옵티마이저에도 종류가 여러가지 있는데
이부분은 다음 게시글에서 알아보도록 하겠다!
참고자료
혁펜하임의 “꽂히는” 딥러닝 (Deep Learning) 1-1 강. 선형 회귀
'AI > ML,DL' 카테고리의 다른 글
| [ML/DL] 소프트맥스 회귀(Softmax regression) (0) | 2022.12.16 |
|---|---|
| [ML/DL] 로지스틱 회귀(Logistic Regression) (0) | 2022.12.15 |
| [ML/DL] 인공신경망(Artificial Neural Network), 활성화 함수(Activation Function) (0) | 2022.12.14 |
| [ML/DL] 경사하강법(Gradient Descent), 뉴턴-랩슨법(Newton-Raphson) (0) | 2022.12.13 |




