Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- the longest increasing subsequence
- pcce 기출문제 풀이
- boj 6443
- making anagrams
- find the town judge
- pccp 기출문제 풀이
- ice cream parlor
- gas
- count triplets
- 브루트포스
- DirectX
- LCS
- the maximum subarray
- 프로그래밍공부
- boj 1074
- boj 1717
- 2025 프로그래머스 코딩챌린지 1차예선
- c++
- lock based stack
- PCCE
- two characters
- DirectX12
- dp
- 지게차와 크레인
- special string again
- lock free stack
- find the running median
- boj 11657
- lock based queue
- string construction
Archives
- Today
- Total
오구의코딩모험
[Python] 위장 본문
반응형

[코딩테스트 고득점KIT - 해시]

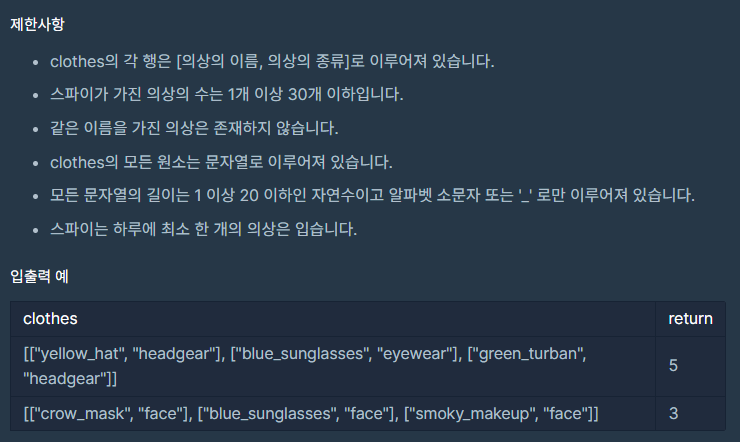
처음엔 combination 을 이용하여 풀었지만,
정확성 테스트 케이스는 모두 통과하나 효율성 테스트를 시간초과로 통과하지 못하였다.
의상의 종류를 담기 위해 clo 리스트를 생성하고 값을 넣는다.
Counter 라이브러리를 이용하여 의상 종류별 count를 해준다.
ex) Counter({ headgear : 2, eyewear : 3, face : 1})
여기서 각 카운트 값을 +1 해준 후,
reduce 함수를 통해 각 카운트 값을 전부 곱해준다.
그리고 -1 까지..
이유는
다른 분의 설명을 참고하도록 하겠다..
만약에 옷의 종류가 1개라고 해봅시다.
개수는 a개입니다. 그럼 총 a가지의 경우가 있겠죠?
종류가 2개가 되고 각각의 옷의 개수는 a, b개입니다.
그럼 경우의 수는 a, b, ab가 되므로 조합의 개수는 (a+b) + (ab)가지입니다.
3개가 된다면? (a+b+c) + (ab+bc+ca) + (abc)가지입니다.
어디서 많이 보시지 않았나요?
학창시절에 우리는 다항식을 배우는데 위의 가짓수는 n차식(n = 옷의 종류의 개수) 계수들의 합입니다.
즉, 옷의 종류가 3가지고 각각의 옷의 개수가 a, b, c라면 (x+a)(x+b)(x+c) = x3 + (a+b+c)x2 + (ab+bc+ca)x + (abc)라는 식이 정립됩니다.
보이시죠? 총 조합의 개수가 계수에 다 포함되어 있습니다.
해당 식의 계수의 합을 구하려면 x=1을 대입해주면 됩니다.
그 후 맨 앞 x3 의 계수는 정답에 포함되지 않으므로 마지막에 1을 빼주는 겁니다.
x=1을 대입한 식은 (1+a)(1+b)(1+c)가 되고 그 값에 1을 뺀 후 리턴해주면, 정답이 나오는 이유가 그것입니다.
https://school.programmers.co.kr/questions/33347
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
요약하자면,
n개의 의상 종류의 경우의 수는
(n차 다항식 계수의 곱) - 1과 같다.
from collections import Counter
from functools import reduce
def solution(clothes):
clo = [clothe[1] for clothe in clothes]
answer = len(clo)
cnt = Counter(clo).values()
cnt = list(map(lambda x : x+1, cnt))
answer = reduce(lambda x, y: x * y, cnt) - 1
return answer
반응형
'프로그래밍 공부 > 프로그래머스' 카테고리의 다른 글
| [Python] 올바른 괄호 (0) | 2022.12.24 |
|---|---|
| [Python] 같은 숫자는 싫어 (0) | 2022.12.24 |
| [Python] 전화번호 목록 (0) | 2022.12.23 |
| [Python] 베스트앨범 (0) | 2022.12.22 |
| [Python] 폰켓몬 (1) | 2022.12.14 |
Comments




