| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- DirectX
- pccp 기출문제 풀이
- lock based stack
- boj 1717
- string construction
- 프로그래밍공부
- 지게차와 크레인
- special string again
- LCS
- PCCE
- count triplets
- boj 6443
- pcce 기출문제 풀이
- find the town judge
- lock free stack
- 2025 프로그래머스 코딩챌린지 1차예선
- c++
- ice cream parlor
- the longest increasing subsequence
- DirectX12
- two characters
- making anagrams
- dp
- 브루트포스
- boj 1074
- lock based queue
- boj 11657
- find the running median
- gas
- the maximum subarray
- Today
- Total
오구의코딩모험
[C++] BOJ 20444번 : 색종이와 가위 본문


https://www.acmicpc.net/problem/20444
문제 3줄 요약
1. 직사각형의 색종이를 가위로 자른다.
2. 한 변에 평행하게 자르며, 자를 땐 멈추지 않고 자른다.
3. n번의 가위질로 k개의 색종이로 자를 수 있는지 확인하는 코드를 작성하자.
예시를 통해 살펴보자!
4번의 가위질로 9개의 색종이를 만든다면?

위의 그림과 같이
가로 2번, 세로 2번을 자른다면 9개의 색종이로 자를 수 있다.
따라서
가로로 몇 번을 자르는지,
세로로 몇 번을 자르는지에 따라서
몇 개의 색종이로 나뉘어 지는지 계산이 가능하다.
계산식을 작성해본다면
가로로 자른 횟수 : x
세로로 자른 횟수 : 전체 가위질 - x
색종이 수 = ( x + 1 ) * ( n - x + 1 )
로 표현할 수 있다.
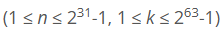
그럼 이 식을 어떤 식으로 탐색해야
위의 범위를 시간 초과없이 풀 수 있을까?
세로로 자른 횟수를 0회부터 최대 횟수의 n회까지의
색종이 총 개수를 이분 탐색으로 k 값에 유사하게 도달하고자 한다.
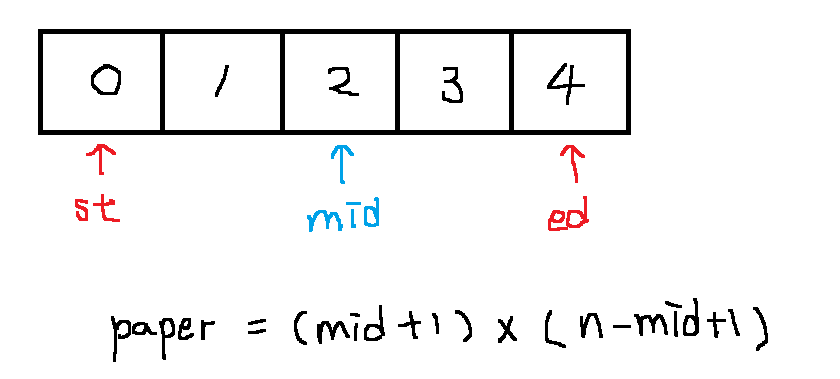
위의 예시에 첫 번째 탐색은
최소인 0과 최대인 4의 mid(중간값)인 2회를 기준으로 탐색한다.
따라서
색종이의 개수는
( 2 + 1 ) * ( 4 - 2 + 1 ) = 9이다.
첫 중간 값이 k 값과 동일하여 탐색을 중단하여도 되지만
필자는 k 값을 만들 수 없는 경우까지 고려하여
st 값이 타겟 값과 가장 유사하게 이동하도록 한다.

따라서
ed 값을 중간값으로 이동시킨다.
만일 중간값이 k 값보다 작으면 st 값을 중간값보다 앞으로 이동한다.
이후 st와 ed 값은 아래와 같이 이동한다.
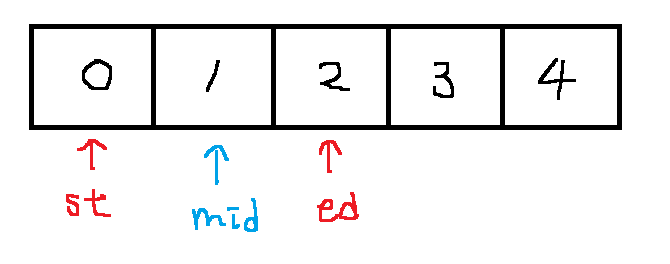
중간값의 색종이 개수가 k값 보다 작기 때문에
st는 mid+1로 이동한다.
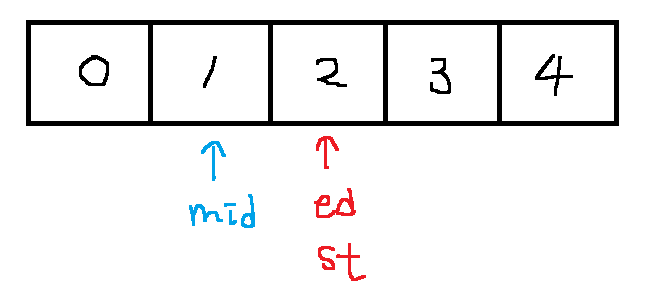
st와 ed이 같은 위치에 도달하며
이분탐색을 종료한다.
이후 탐색한 st 값을 기준으로
계산한 paper의 값이 k와 같다면 k개의 색종이를 만들 수 있는 경우이다.
위의 의사코드를 작성하면
아래와 같다.
#include <iostream>
using namespace std;
int main(void){
ios::sync_with_stdio(0); // c stream, c++ stream 중 c++ stream만 사용
cin.tie(0); // 버퍼 비우지 않음
long long n, k;
cin >> n >> k;
// 한 방향을 기준으로 자르기
long long st=0, ed=n;
while(st < ed)
{
long long mid = (st+ed)/2;
long long paper = (mid+1)*(n-mid+1);
if(paper >= k) ed = mid;
else st = mid+1;
}
if((st+1)*(n-st+1) == k) cout << "YES";
else cout << "NO";
return 0;
}
이분 탐색이 생각보다 단순하지가 않고
파생되는 개념이 많아보인다.
다음엔 이분 탐색에 대한 개념을
자세히 정리해보겠다.
끝!

'프로그래밍 공부 > 백준 알고리즘' 카테고리의 다른 글
| [C++] BOJ 1074 : Z (0) | 2025.03.29 |
|---|---|
| [C++] BOJ 6443번 : 애너그램 (0) | 2025.03.24 |
| [C++] BOJ 20207번 : 달력 (0) | 2025.02.19 |
| [C++] BOJ 21921번 : 블로그 (0) | 2025.02.16 |
| [C++] BOJ 11053번 : 가장 긴 증가하는 수열 (LIS) (0) | 2025.02.15 |




