| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- boj 11657
- dp
- 비밀 코드 해독
- DirectX
- lock free stack
- lock based stack
- the longest increasing subsequence
- 프로그래밍공부
- pcce 기출문제 풀이
- c++
- two characters
- 브루트포스
- DirectX12
- special string again
- 2025 프로그래머스 코딩챌린지 1차예선
- boj 1074
- count triplets
- boj 1717
- find the running median
- string construction
- lock based queue
- the maximum subarray
- ice cream parlor
- making anagrams
- 지게차와 크레인
- pccp 기출문제 풀이
- boj 6443
- find the town judge
- PCCE
- LCS
- Today
- Total
오구의코딩모험
[Python] 2485번 : 가로수 본문

https://www.acmicpc.net/problem/2485
2485번: 가로수
첫째 줄에는 이미 심어져 있는 가로수의 수를 나타내는 하나의 정수 N이 주어진다(3 ≤ N ≤ 100,000). 둘째 줄부터 N개의 줄에는 각 줄마다 심어져 있는 가로수의 위치가 양의 정수로 주어지며, 가
www.acmicpc.net
문제 3줄 요약
1. 가로수가 임의의 간격을 두며 직선으로 배치 되어있다.
2. 가로수를 더 심어 모든 가로수들의 간격을 같게 한다.
3. 가로수를 최소로 심어 간격을 같게 할 경우, 몇 개 심어야 할까?
그림판을 키고,
그림으로 문제의 이해를 돕도록 하겠다.
가로수들의 위치가
한 줄에 하나씩 좌표로 주어진다.
Ex) 1, 3, 7, 13 일 경우
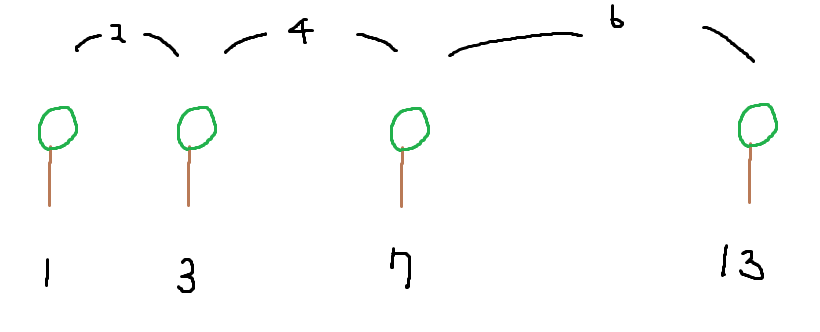
위의 그림처럼 표현할 수 있고,
간격이 2, 4, 6 이란 것을 알 수 있다.
그럼 몇 개를 더 심어야 할까?
직관적으로 간격을 봤을 때,

위 그림처럼 5, 9, 11에 추가를 해주면
간격을 2 씩 두고 있는 가로수를 만들 수 있을 것이다.
왜 2 일까?
우린 간격이 2, 4, 6으로 떨어져 있는 가로수를 채워야하고
그렇다면 2, 4, 6을 나눴을 때,
모두 나누어 떨어지는 숫자로 간격을 배치해야하며,
또한 최소 간격인 2보다는 작거나 같아야 할 것이다.
만약 2 보다 크다면?
1, 3 가로수 배치부터 실패!
위의 설명한 것을
수학적으로 접근해본다면,
간격의 차이인 2, 4, 6
이 세 정수의 공약수 중 가장 큰
최대공약수인 2가 간격의 최대가 되겠다!
from sys import stdin
import math
N = int(stdin.readline())
# tree : 가로수 좌표 리스트
# gap_list : 가로수 간격 리스트
# gcd : 최대공약수
tree, gap_list, gcd = [], [], 0
# 가로수 좌표 리스트
for idx in range(N):
tree.append(int(stdin.readline()))
# 가로수 좌표가 오름차순이 아닐 수 있으니,
# 오름차순 정렬
tree = sorted(tree)
# 좌표 리스트
# 멀리 있는 가로수 좌표에서 가까운 가로수 좌표를 뺀다.
for idx in range(N):
if idx != 0:
gap = tree[idx]-tree[idx-1]
gap_list.append(gap)
# 간격 차이 중복 제거
set_gap = list(set(gap_list))
# 중복 제거 후,
# 남은 간격 차이가 하나라면, 간격이 동일한 것
if len(set_gap) > 1:
gcd = math.gcd(set_gap[0], set_gap[1])
for idx in range(2,len(set_gap)):
gcd = math.gcd(set_gap[idx], gcd)
print(sum([distance//gcd-1 for distance in gap_list]))
else:
print(sum([distance//set_gap[0]-1 for distance in gap_list]))
예외 상황인
모두 간격이 같은 경우와
좌표가 오름차순으로 주어지지 않은 경우만 처리해준다면,
끝!
오늘 그림판 그림 좀 잘그린듯?

'프로그래밍 공부 > 백준 알고리즘' 카테고리의 다른 글
| [Python] 15711번 : 환상의 짝꿍 (0) | 2023.03.08 |
|---|---|
| [Python] 6588번 : 골드바흐의 추측 (2) | 2023.03.07 |
| [Python] 14889번 : 스타트와 링크 (0) | 2023.03.04 |
| [Python] 2661번 : 좋은 수열 (0) | 2023.03.04 |
| [Python] 1182번 : 부분수열의 합 (0) | 2023.03.02 |





